今回の課題は以下の様な図面です。

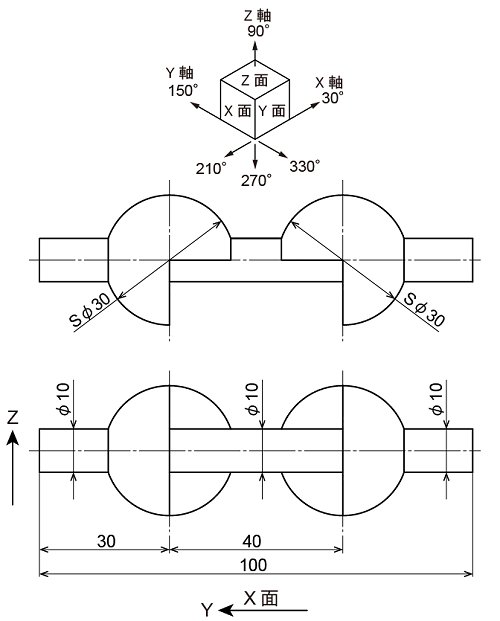
※上記図面の平面図が間違っていたので修正しました。(2021/05/17)

２つの同じ大きさの半断面の球が向き合っている状態を、直径１０ｍｍの丸棒が貫いている形状です。

半断面の書き方と、貫いた丸棒との境界線が球の表面のどの位置に現れるかが考えさせられる所でしょうか。

それでは書いていきます。

まず、球を１つ書き、同じ大きさの３５°楕円を中心に書きます。

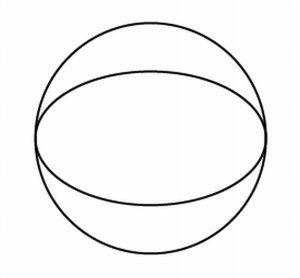
３５°楕円を１２０度ずつ２回回転コピーします。

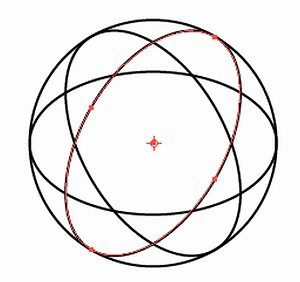
全体を４０ｍｍ/３３０°方向へコピーします。

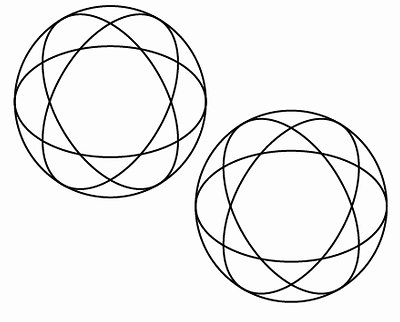
丸棒を書きます。

右下の球の中心に、１０ｍｍ/３５°楕円を書きます。

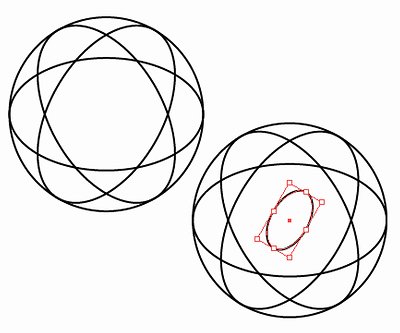
３０ｍｍ/３３０°方向にコピーし、さらにそれを１００ｍｍ/１５０°方向にコピーします。

丸棒の稜線をひき、丸棒を完成させます。

最初に書いた３５°楕円を４０ｍｍ/１５０°方向にコピーします。

 

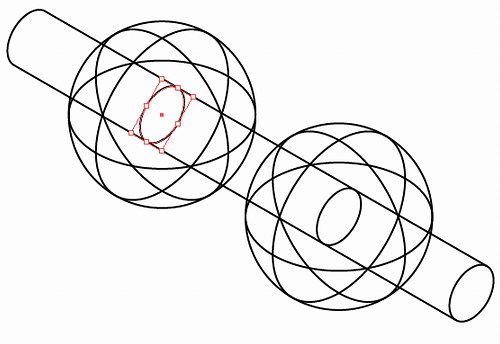
奥側の球の半断面の境界となる垂直線を引きます。

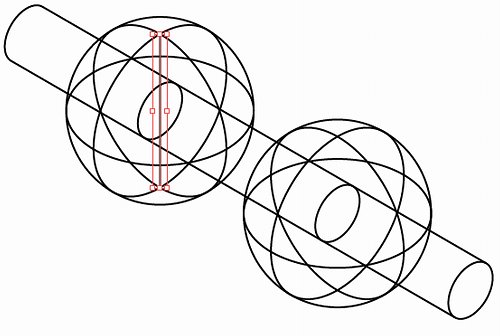
楕円および球の不要部分を削除します。

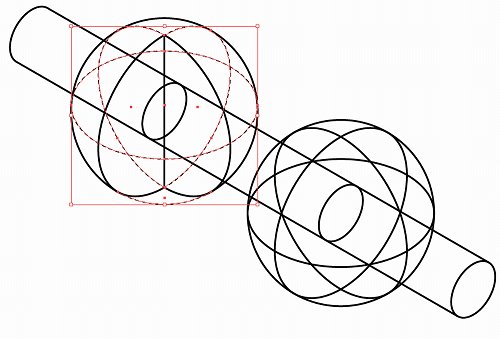
境界線と楕円の交点から３３０°方向へ直線を引き、球の表面との交点を求めます。

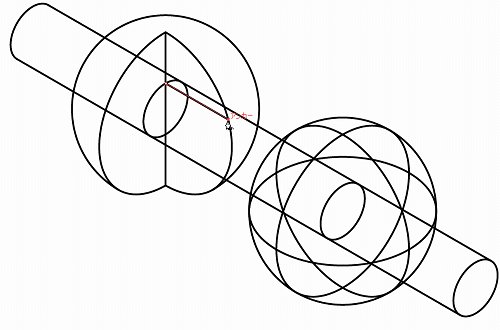
その交点に楕円をコピーします。ここが楕円と球の交わる位置です。

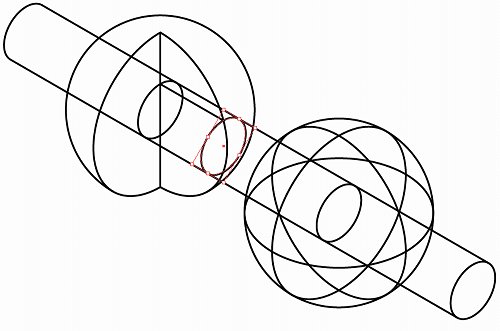
不要部分を消して、奥側の球を完成させます。

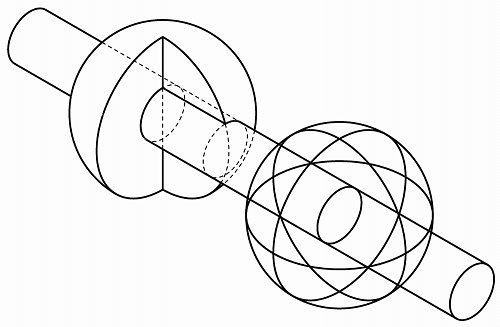
下図の様に断面と丸棒が交わる直線を延長して、手前の球の半断面との交点まで伸ばします。

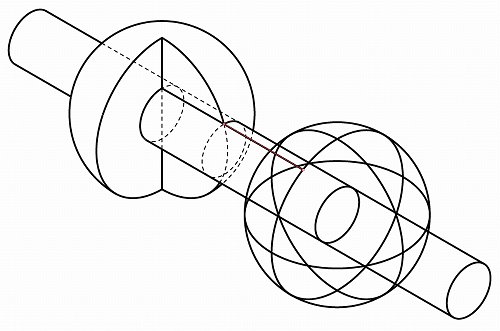
不要な線を整理します。

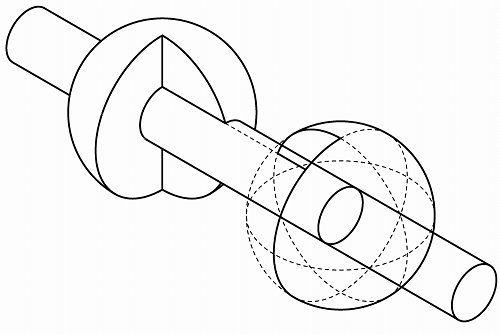
先程と同じように、３５°楕円を３３０°方向に移動して球と丸棒の交わる位置を求めます。

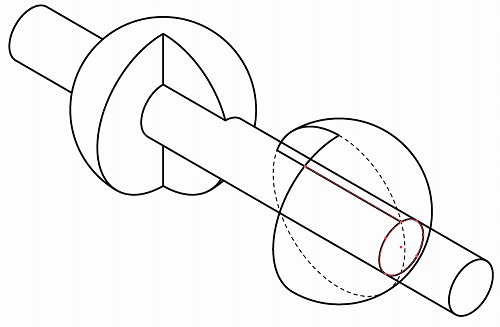
不要部分を削除します。

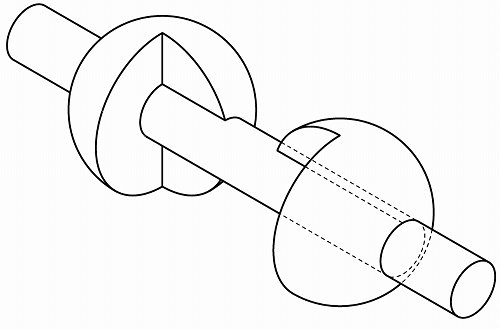
整理して完成です。

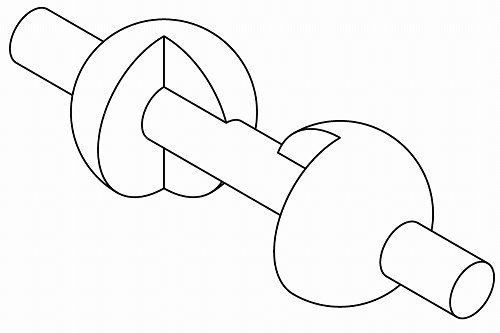
では。