今回は、接合部の丸みについてです。
今現在(2021.05.22)まで、本ホームページでは2つの形状がくっついている場合の接合部に丸みのある形状は掲載してきませんでした。
特に理由は無いのですが...。
そこで今回はその辺の考え方についてです。
例えば以下の様な図面を見てみましょう。
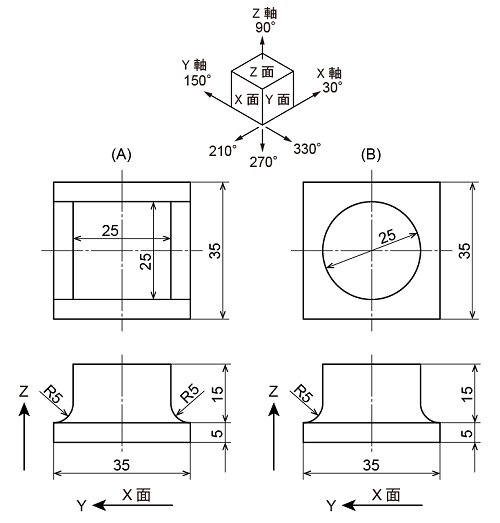
(A)は、四角い板の上に四角いブロックが乗っていますが、そのくっつく部分にR5の丸みが付いています。
側面図は無いので、正面図から見た方向のみにR5があります。
(B)は、やはり四角い板の上に今度は円柱が乗っていますが、同様にR5の丸みが接合部にあります。
円柱ですので1週ぐるっと丸みがある事になります。
それでは書いてみましょう。
(A)からです。
普通に丸みが無いものとして書いてみますと以下の様ですね。
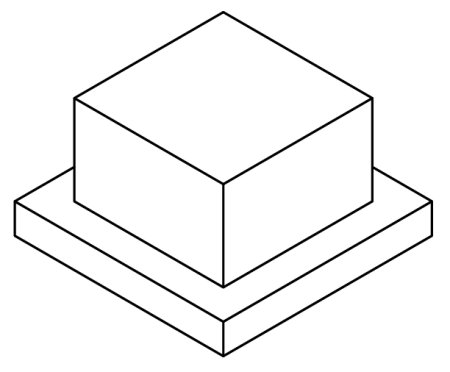
正面がX面ですので、X面上の円形(丸みは円形の一部と考えられます)は以下の様な35°楕円と考えられます。
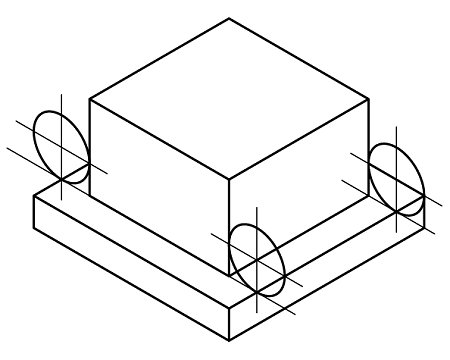
これを整理しますと...
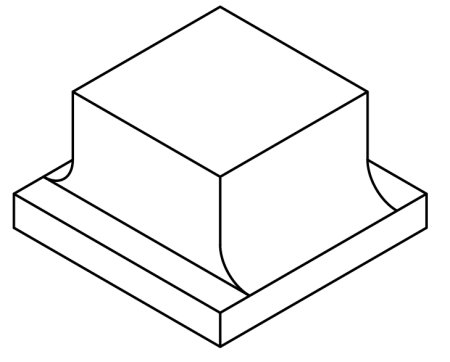
こんな感じになります。
次に、(B)です。
(B)も丸みが無いものとして書いてみますと以下の様ですね。
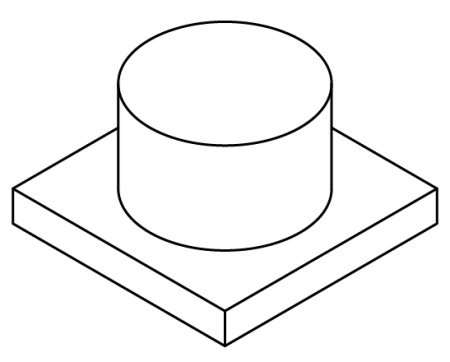
円柱の場合は、平面ではないのでX面の35°楕円という考え方はできません。
接合部の丸みが現れるのは正面を向いている部分です。
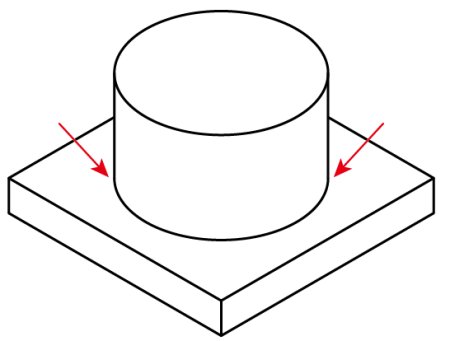
こういう、正面を向いている部分に使う楕円は55°楕円という楕円度の物を使います。
このサイトは今まで正円(球)と35°楕円しか使ってきませんでしたが、当然角度の付いたところの丸みには他の楕円度の物を使う事になります。
その辺の楕円度については、いづれどこかで書くと思います...。
とりあえず、今回のような部分に使うのは55°楕円と覚えてしまって構わないと思います。
正円でも良いような気がしますが(正円で書いてもさして違いは無いのですが...)、丸みを楕円として考えると45°上方から見ているので円はつぶれますね。
では、55°楕円ってどんな楕円?となりますよね。
55°楕円の作り方です。
まず直径10mmの正円を書き、122%に拡大します。
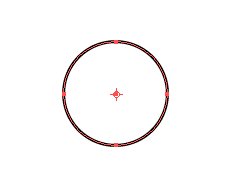
中心線を書きます。
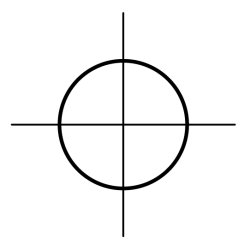
円の中心から右方向に直線を書き、円の中心を回転中心として55°回転させます。
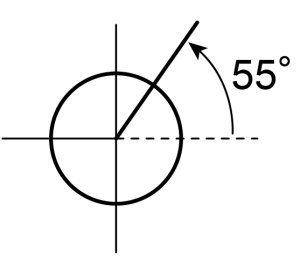
その線と円の交点から、垂直の中心線へ水平線を引きます。
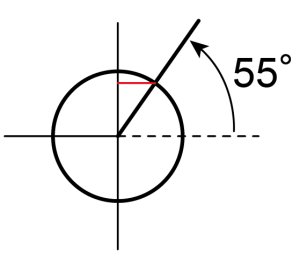
円を選択ツール(黒矢印)で選択し、上のアンカーポイントをAltキーを押しながらドラッグして今書いた赤い線と垂直の中心線の交点までつぶします。
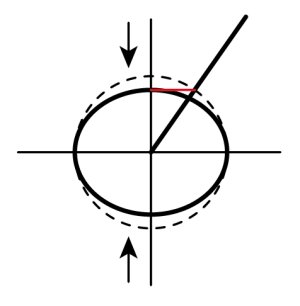
出来た楕円が55°楕円です。
これを先程のイラストに適用します。
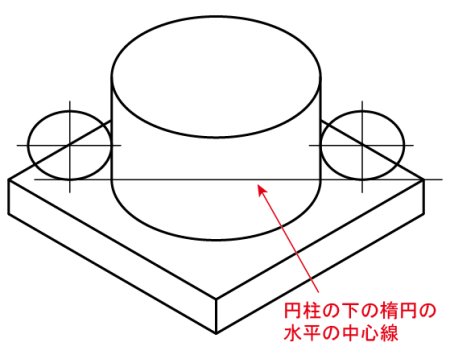
くっつける時に、基本的には円柱の下の楕円の水平の中心線に接合させることに気を付けてください。
斜め上から見ているので、Rはもう少し上でも良いのかもしれませんが...。
不要部分を削除します。
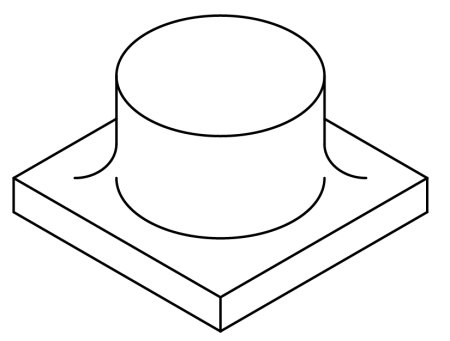
残った円柱の下の楕円の処理(実際の形状にはここの線はありませんね)は、人によっても参考書によっても様々です。
つまり正解はありません。
例えば以下の様な表現の場合もあります。
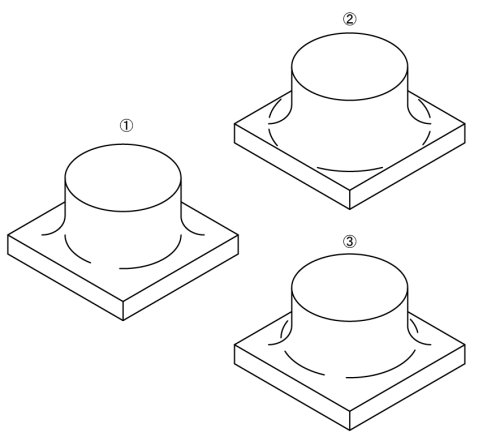
他にもありそうですが、私は大抵上の①で書きます。
では。
 |
 |
 |
 |

